Here’s a challenge which appeared in a German chess magazine in 1848: place eight white queens on an empty chessboard so that no two queens occupy the same file, rank or diagonal. In other words, none of the queens may defend each other.
Perhaps you start with a queen in the top left corner, on a8. The next might be placed on the adjacent file, nearby but not touching, on the b6 square, a knight’s move away from the first. Following the pattern, you put another on c4, and a fourth one on d2. For the e-file, we need to break the pattern, so let’s revert to near the top of the board, on e7. Flushed with success, you see that the ‘knight move’ pattern still works, and plonk two more queens on f5 and g3. Giddily, you add the last queen on h1, the only unused file and rank, and — bloody hell! — it conflicts with the first queen you placed on a8. This is, as Sherlock Holmes might say, a three-pipe problem.
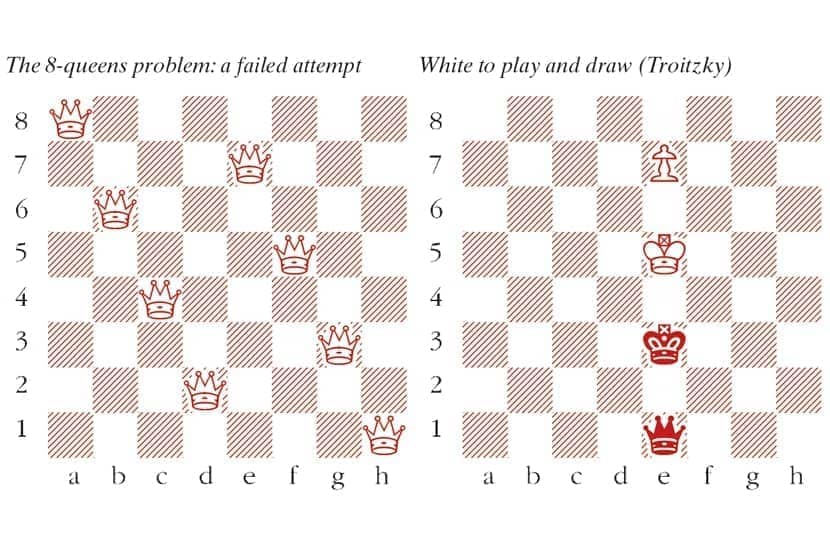
The 8-queens problem: a failed attempt (Diagram above left)
It turns out that there are 92 different solutions, though only 12 of these are fundamentally distinct, once you take into account reflections and rotations. You might wonder how many solutions there are on boards of different sizes — 10×10, or 100×100. In fact, this ‘n queens’ problem (where n denotes a board of arbitrary size) has turned out to be a rich seam for mathematicians. Last year Michael Simkin, a Harvard academic, identified a formula which approximates the number of solutions on giant boards. He found that when n becomes large enough, there are roughly (0.143n)n solutions, which on a 1 million by 1 million board equates to 1 followed by more than 5 million zeros.
On a regular chessboard, trial and error might suffice to find a solution. But the research breakthrough depended on some abstract insights. One key observation is that not all squares are equally likely to be occupied. For example, a queen on one of the four central squares covers 27 squares, while a queen in a corner (or next to a corner) covers just 21. So adding a queen near the corner keeps more options open for subsequent queens. I believe that another point of the algorithm devised by Simkin is that even if a plausible configuration hits a dead end, it may still yield a solution after some modest adjustments.
White to play and draw (Troitzky) (Diagram above right)
In normal chess, the geometrical constraints of the chessboard can create surprising effects too. I found the position in the diagram above in Understanding Queen Endgames (Müller & Konoval, Russell Enterprises 2021). It shows the conclusion of a study composed by the great Alexey Troitzky in 1935. White must find a way to draw, but 1 e8=Q? loses to a discovered check when Black moves the king. And 1 Kf6 loses slowly: 1…Kd4 2 Kf7 Qf1+ 3 Kg7 Qb5 4 Kf7 Qf5+ 5 Kg7 Qe6 6 Kf8 Qf6+ 7 Ke8 Kd5 and Black soon wins the pawn.
The only way to draw is 1 Ke6!, intending 1…Kf4+ 2 Kf7! or 1…Kd4+ 2 Kd7! In either case, Black has no further checks, so the pawn can promote.





Comments