Dante’s millions

As I write, the London world championship is tied at 3½-3½, after seven games. In striving to move ahead, the challenger, Fabiano Caruana, has been the victim of the awesome mathematics of chess. According to the statisticians there are more possible moves in chess games than there are atoms in the observable universe. Ten to the power of 70 is the official estimate. As someone with a good Italian name and ancestry, Fabiano may be familiar with Dante’s Paradiso. In Canto 28 the poet writes: ‘Ed eran tante, che ‘l numero loro, Piu che ‘l doppiar de li scacchi s’inmilla.’ In other words, the number of angels or intelligences in the heavens far exceeds the immense number created by placing a piece of corn on the first square of the chessboard and doubling each time until square 64 is reached. The number of grains on this square alone will be 18,446,744,073,709,551,616 and the total number of grains on the chessboard will be 36,893,488,147,419,103,231.
 
In game six, Caruana conducted a perfect queenless middlegame against the champion, Magnus Carlsen, to reach a winning position. Only then did he falter and miss the win. This was hardly surprising, since it involved finding, among the myriad alternatives, the narrow and unique path to a most counter-intuitive sequence leading to a forced checkmate in more than 30 moves. (The correct sequence was found by the chess engine Stockfish running on the powerful Sesse mainframe computer.)
 
As Garry Kasparov rightly said, if Caruana had found this esoteric solution at the board, then it would have been time for the arbiters to call in the metal detectors! In over-the-board combat, with the clock ticking, the human brain is simply not equipped to penetrate such arcane mysteries of the quasi-infinite numerology of chess.
 
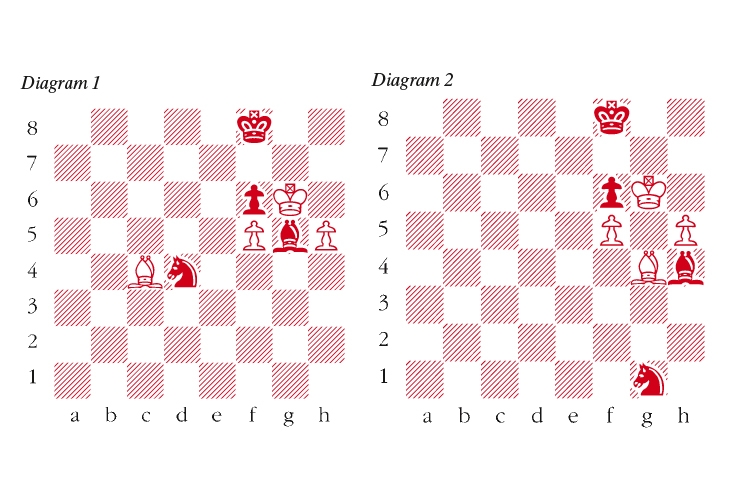
Carlsen-Caruana, World Championship, Game 6, London 2018 (see diagram 1)
 
Here Caruana continued with 68 … Nf3 after which Carlsen’s kingside blockade proved to be sufficient to draw the game.